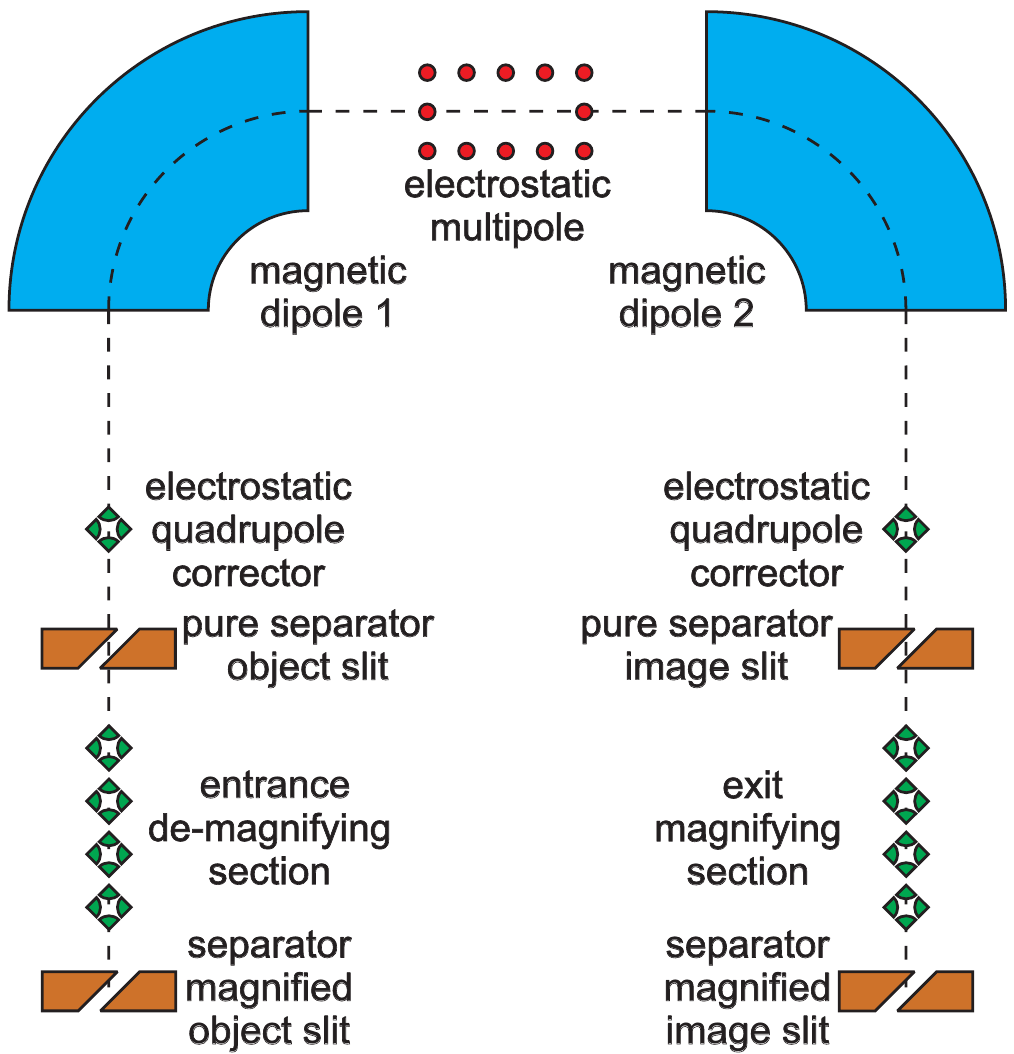
The Optimization Algorithm
The algorithm used to tune the HRS Multipole aims to minimize the distance
between the components composing the centroid of the beam and the center of
the beam. It takes advantage of a superposition trait of the
multipole that can be stated by first making the following definitions.
- $\phi_{i}$ is the potential on the $i^{th}$ electrode pair
- $x_{I}(x')$ is the initial position of the centroid at a given $x'$
- $x_{F}(x')$ is the new position of the centroid at the given $x'$
- $\Delta{x}_{i}(x')$ is the change in position at a given $x'$ caused by applying a 1V potential to the $i^{th}$ electrode pair
The CANREB HRS